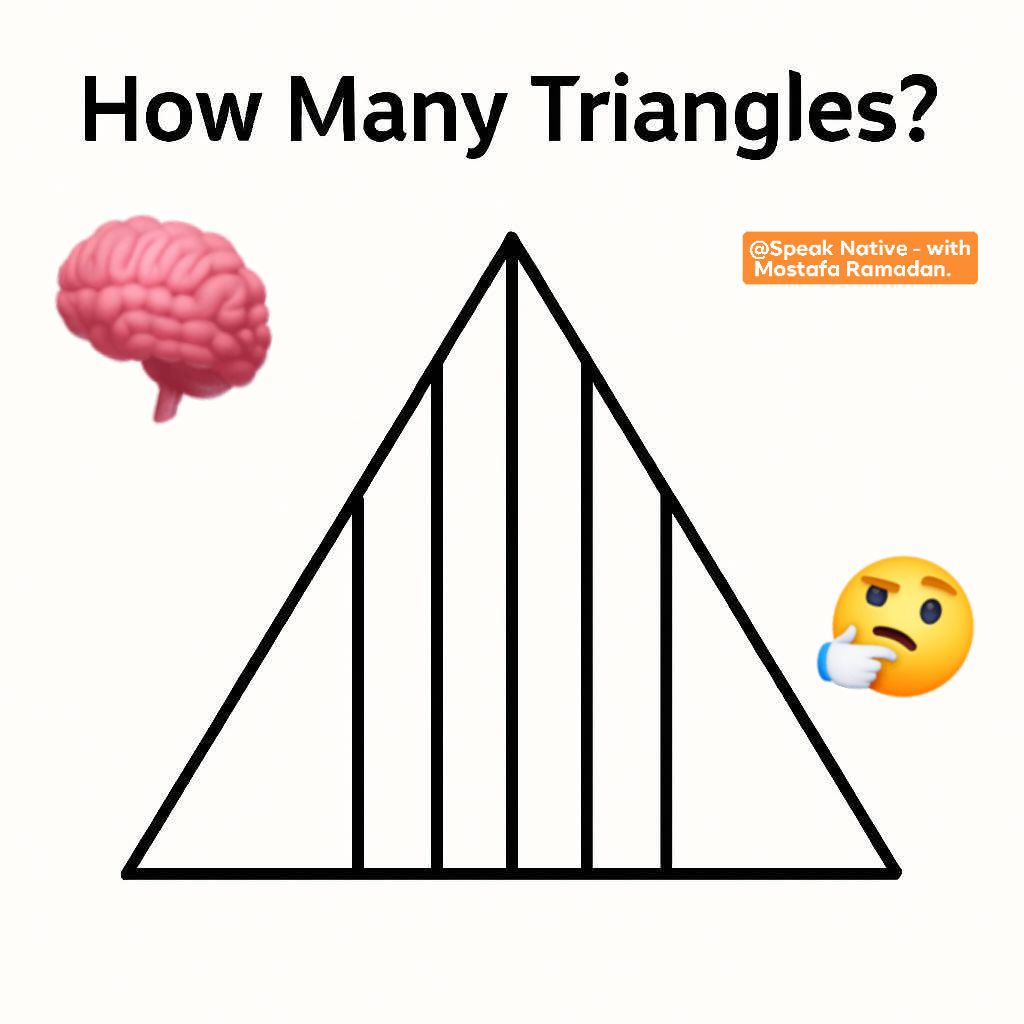
The Deceptive Simplicity: A Forest of Triangles in Plain Sight
The image presents a challenge as classic as geometry itself, distilled into a single, stark line of text on a plain background: How Many Triangles?
There are no accompanying diagrams, no complex interlocking shapes, no shaded figures to analyze. There is only the question. And yet, this very absence is what gives the prompt its peculiar power. It is an empty frame, and our minds immediately rush to fill it.
We do not see a blank space; we see the ghost of every “how many triangles?” puzzle we have ever encountered. We mentally conjure a star made of overlapping lines, a pyramid subdivided into smaller ones, a simple square bisected by two diagonals. The question acts as a Rorschach test for our puzzle-solving memory. The brain, eager for the task, begins drafting hypothetical shapes and counting invisible vertices and edges.
This is the first layer of the puzzle: the puzzle of expectation. Without a visual, the challenge becomes meta-cognitive. It asks: What is the most common, the most devious, the most iconic “triangle count” problem you know? The solver is forced to guess the intent of the asker. Is this a trick of overlapping lines, where smaller triangles hide within larger ones? Is it a question about arrangements of dots, where triangles are formed by connecting non-collinear points? The lack of specification means the answer could be anything from “three” (the minimum to form one triangle) to a number in the dozens, depending on the unseen figure.